Maximum-likelihood classification with a constraint on the class distribution
In supervised classification problems, predictions are usually generated for each sample independently of the others.
A Linear Assignment Problem (LAP) approach to setting population distribution constraints
In supervised classification problems, predictions are usually generated for each sample independently of the others. Consider a scenario where you are classifying images as being either of a “domestic cat” or a “wild cat”. The model evaluates each image on its own, determining whether it’s more likely to depict a domestic cat or a wild cat. Once all images are classified, the resulting class distribution should, ideally, approximate the true distribution of these two types of cats in your image set. But what if this isn’t the case?
Let’s say the images you’re dealing with are mostly of domestic cats, a fact reflected in your training data. However, the actual world distribution between domestic cats and wild cats is not as skewed. In such a situation, your model, influenced by the training data, might be predisposed to predict “domestic cat” more frequently. This could lead to an imbalance in your model’s predictions.
If your image classifier persistently over-predicts the “domestic cat” class, despite efforts like resampling the data or adjusting loss function weights, you’ll want to address this known bias. This imbalance often arises when the available signals in the data — like colour, shape, and size — are not discriminant enough to reliably differentiate between domestic and wild cats. By reinforcing stricter guarantees on the population-level class distribution, we can counter these issues and extract the maximum value from our model.
Alternatively, if you have a separate model that accurately predicts the overall population distribution between domestic and wild cats, you might want to combine this model with your image classifier to better reflect the true distribution.
Now for the good news: there is a simple way to optimally adjust for a desired population class distribution, without any changes to your classifier model! To see how this works, let’s look at a simple example.
In this example, we are classifying seven samples (s1, s2, …, s7) into three classes: blue, red, and green. At a population level, blue is the most common class (57%), followed by red (29%) and green (14%).
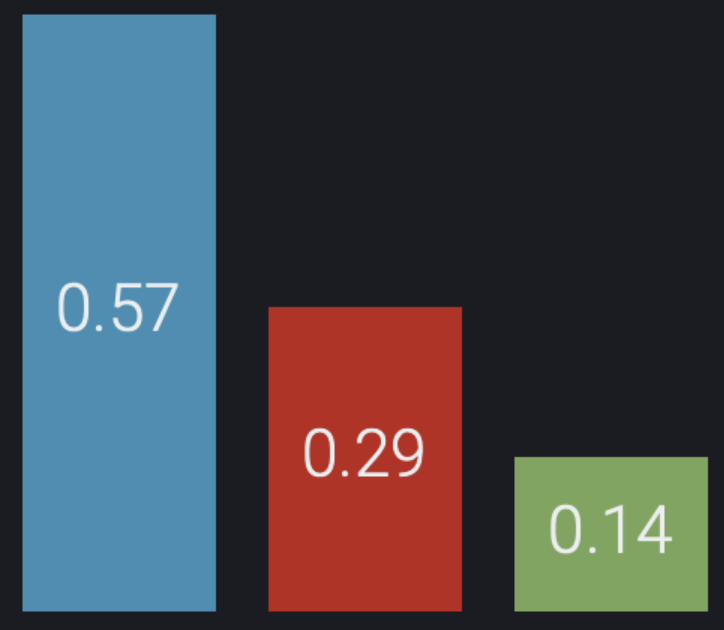
However, the trained model in this example is unable to reliably identify which of the seven samples are red or green. There is potentially meaningful variability in the predicted probabilities, but in every case the highest probability is for blue:

Figure 2: predicted probabilities by the classifier model
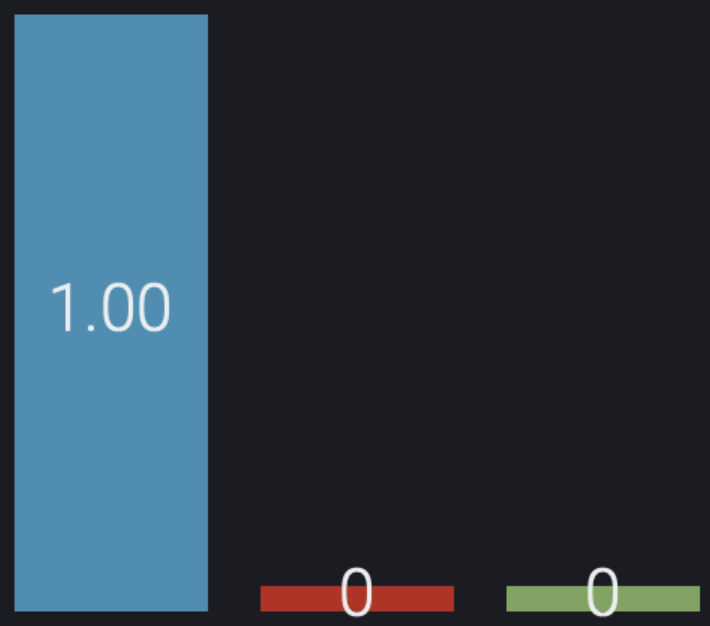
If we take the usual Maximum Likelihood approach and select the class with the highest probability for each sample independently of the others, then we end up with a highly imbalanced distribution:
Before proceeding with this example, we will take a quick detour and talk about something slightly different — the Linear Assignment Problem (LAP). The LAP is a classic combinatorial optimisation problem that can be framed in terms of assigning n jobs to n workers, where each job can only be performed by exactly one worker, and each worker-to-job assignment has an associated cost. For example:
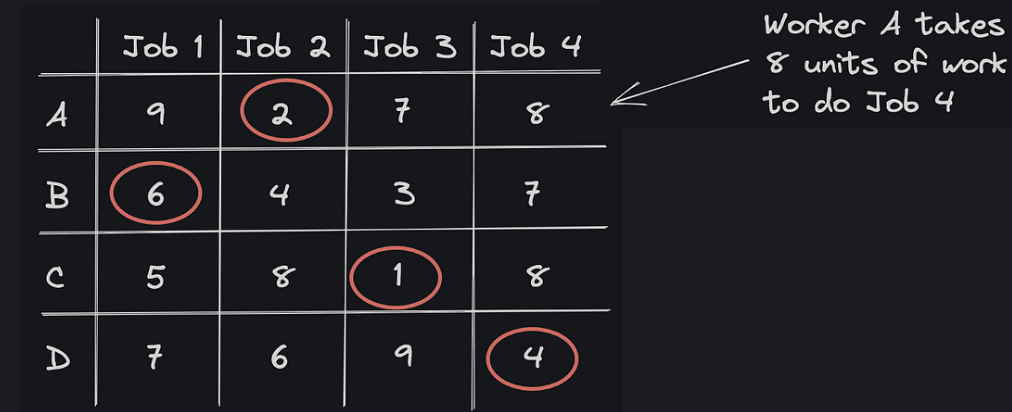
Figure 4: example Linear Assignment Problem with 4 jobs and 4 workers
For the example in Fig. 4 above, the optimal assignment of jobs that minimises the total cost is indicated by the red circles — worker A does job 2 (cost = 2), worker B does job 1 (cost = 6), etc. Luckily there are many algorithms for solving the LAP, one of the fastest ones being the Jonker-Volgenant algorithm. The Jonker-Volgenant algorithm finds the globally optimal solution for LAPs with a worst-case time complexity of O(n3). A Python implementation is available through scipy: scipy.optimize.linear_sum_assignment.
Now for the big reveal: it turns out we can reframe our classification problem as a LAP, harnessing the power of the Jonker-Volgenant algorithm to find a globally optimal assignment of classes that conforms to a desired population distribution. Here’s how (example code given at the end):
First, we create “labels” L with the desired class distribution. We started our example above aiming to achieve a 57–29–14 percent distribution for blue, red, and green, respectively (Fig. 1). This means that, given our population has n=7 samples, we need to create 4 blue, 2 red, and 1 green labels. So, we instantiate labels L1, L2, L3, and L4 with a “blue” value, labels L5 and L6 with a “green” value, and label L7 with a “red” value.
Second, we create an n x n matrix C using the predicted probabilities from the model and the labels created in the first step. The rows in our matrix C corresponds to the samples, the columns correspond to the labels, and each (i,j) entry in the matrix contains the predicted probability of sample si being of the class specified by label Lj: C[i, j] = Prob(si is of class Lj). The matrix C for our example is shown below:
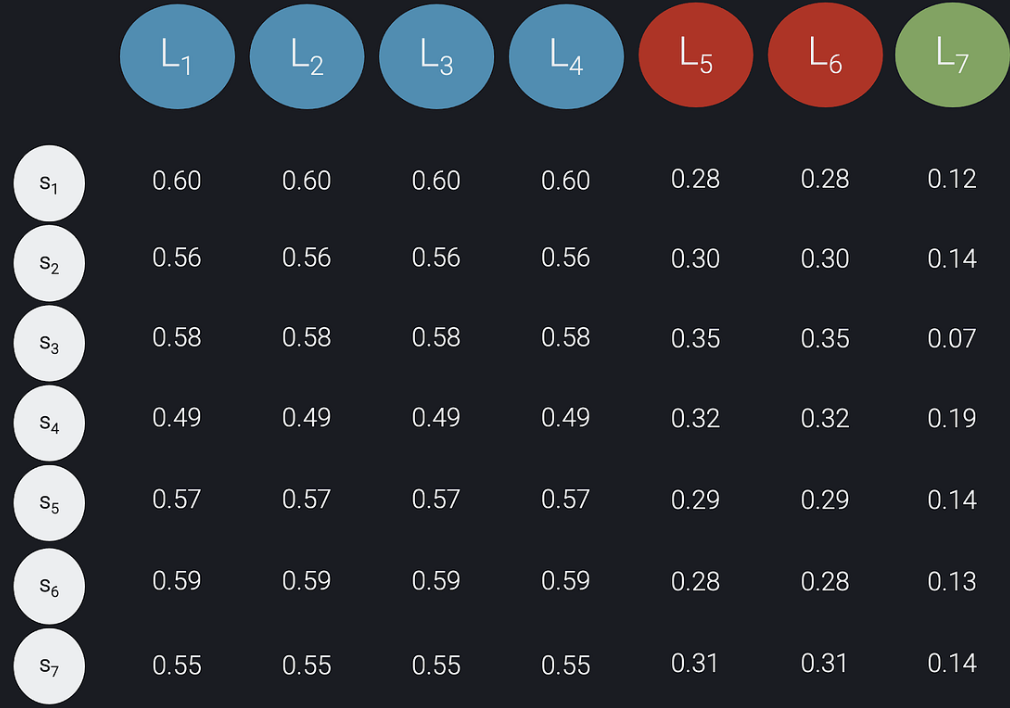
Figure 5: matrix C constructed from the predicted probabilities and the desired class distribution
Finally, we compute the negative log likelihood matrix K = -log C and apply the Jonker-Volgenant algorithm on K to obtain the optimal assignment of labels to subjects. Note that this is equivalent to finding the Maximum Likelihood solution with a constraint on the class distribution. Jonker-Volgenant finds the assignment of labels to samples that minimises the sum of the negative log-probabilities, thereby maximising the product of probabilities. The optimal solution for our example is given below:
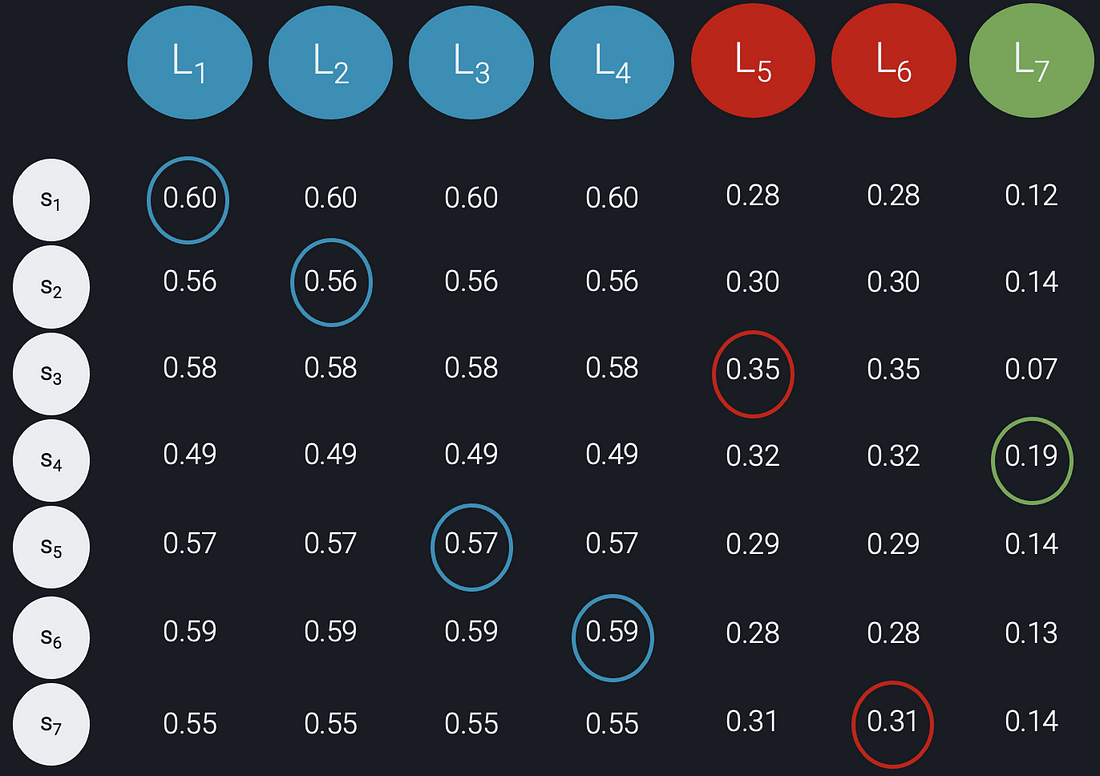
Figure 6: optimal assignment of labels to samples
In conclusion, the application of the Linear Assignment Problem (LAP) using the Jonker-Volgenant algorithm provides a robust solution to address class imbalance in supervised classification tasks. This method allows for combining individual prediction probabilities with a predefined class distribution, thereby maximising the overall likelihood. This approach is particularly beneficial when dealing with skewed distributions and when conventional methods for handling class imbalance are ineffective. By reframing the classification task as a LAP, we unlock a powerful mathematical technique to enforce constraints on the class distribution, without altering the underlying model.
To see the example code, visit this blog on Medium.